| Accueil |
Qui sommes-nous? | Recherches | Actions | Réalisations |
| Thème 1 | Thème 2 | Thème 3 | Thème 4 | Thème 5 |
|
|
Maths à Modeler est une équipe de recherche fondée en 2003. A l'origine, composée de chercheurs en mathématiques discrètes et de chercheurs en didactique des mathématiques, l'équipe compte aussi aujourd'hui des chercheurs d'autres communautés scientifiques venus grossir les rangs au fil des ans. Les disciplines telles que les sciences de l'information et de la communication, les sciences de l'éducation ou encore la psycho-clinique sont désormais représentées. Projet de recherche : une des préoccupations sociétales relatives aux sciences est
souvent formulée comme un problème de désaffection croissante des étudiants vis-à-vis
des filières scientifiques. Si l’on regarde un peu plus en profondeur, on
constate : Le groupe constituant ce projet se veut force de
propositions par l’évaluation et l’analyse de l’existant et la conception et la
réalisation de nouveaux vecteurs de diffusion de la culture scientifique et
technique prenant en compte ces préoccupations. Il est constitué d’acteurs impliqués, depuis plusieurs
années, dans une démarche de popularisation et d’enseignement des mathématiques
: chercheurs en mathématiques et didacticiens des mathématiques. Ce groupe est
complété par des chercheurs d’autres disciplines ayant une approche globale de
l’enseignement, de la communication et de la médiation scientifique : sciences
de l’éducation et sciences de l’information et de la communication. La
méthodologie adoptée repose dans un premier temps dans l’identification de problèmes
de la recherche actuelle susceptibles d’être transposés dans des pratiques
scolaires et des pratiques d’animation et de médiation scientifique. Les
chercheurs en mathématiques discrètes impliqués dans ce projet constituent la
force de proposition des problèmes qui serviront de base aux situations
recherches (SR). En second lieu, la validation de ces situations repose sur
un corpus expérimental de diverses formes : ateliers sur l’année, 6 à 10
séances hebdomadaires ou actions ponctuelles ; dans des cadres scolaires ou
extrascolaires et aussi en formation des formateurs (enseignants du primaire au
supérieur, formateurs d’adultes en difficulté avec les compétences de base). L’ensemble de ces expérimentations permet d’affiner le
travail de transposition didactique afin d’aboutir à une SR. Afin de compléter
ces deux premiers temps qui reposent essentiellement sur des analyses
mathématiques, épistémologique, didactiques et communicationnelles, il convient
d’étudier plus finement les dispositifs de mise en oeuvre : utilisation de
support ludique, analyse du discours de médiation, mise à disposition sur
internet et/ou CDRom, … Les mathématiques sont un domaine de recherche où la
description des résultats et des objets d'étude fait appel à un symbolisme fort.
Notamment le choix des signes et représentants d’une classe d’objets n’est pas
innocent. L’appropriation des signes par l’apprenant est un enjeu crucial dans l’enseignement
des mathématiques. Une des spécificités des mathématiques discrètes est que
souvent un représentant de la classe d’objets s’avère être canonique et peut
être étudié pour déterminer des propriétés sur toute la classe qu’il
représente. Des recherches spécifiques sont entreprises sur ce thème en observant
notamment quel contrôle les apprenants exercent sur les objets mis à leur
disposition. Ces travaux sortent du cadre de l’analyse stricte de la situation
et sont effectués en collaboration avec des chercheurs en sciences de
l’éducation. De façon analogue, l’utilisation d’artefacts dans la médiation scientifique
pour s’affranchir du formalisme peut conduire à des erreurs d’interprétation
et/ou une compréhension incorrecte du discours, mais aussi à des compétences
interprétatives mobilisées de manière non prévisible. Elle peut aussi permettre
de déterminer des différences d’approches entre outils pédagogiques et outils
culturels. Afin d’étudier et d’analyser ce processus nous entreprenons des
expérimentations avec un public spécifique d’enfants en grandes difficultés. En effet, la distance de l’enfant à
l’objet varie selon son développement et l’utilisation d’artefact s’avère être
un obstacle pour certains qui n’est plus de nature épistémologique. Ces
recherches seront entreprises en collaboration avec des chercheurs en sciences
de la communication et en psychologie clinique. Ces recherches pourront
s’enrichir d’expérimentations avec des adultes en difficulté avec les
compétences de base et engagés dans une dynamique de ré-apprentissage. La mise à disposition de ressources de médiation pour un
large public est l’une des préoccupations de chercheurs de notre fédération.
Depuis 2001, nous développons un site web « LA VALISE : maths à modeler » où
nous proposons nous forme de jeux (applet java) des points d’entrée vers des
SR. L’expertise des chercheurs du Gresec autour de l’analyse des ressources
pédagogiques multimédias permet d’étudier les spécificités de La Valise afin
d’identifier les usages, le public utilisateur et dans une certaine mesure
l’impact. Ces questions de recherche sont développées autour de 5 thèmes de recherche : Thème 1. Mathématiques Discrètes (Sylvain Gravier) Thème 4. Situations Recherche hors classe (Marie-Christine Bordeaux) Thème 5. Situations Recherche pour un public spécifique (Serge Manin)
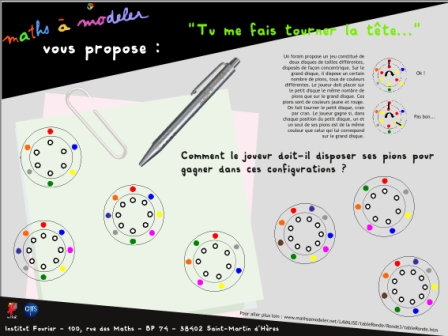
Exemples de situations recherches :
|
|
| Maths à Modeler - Institut Fourier - 100, rue des maths - BP 74 - 38402 Saint-Martin d'Hères - France | ||||
| Maths à Modeler - Institut Fourier - 100, rue des maths - BP 74 - 38402 Saint-Martin d'Hères - France | |
| Mentions Légales | |



|
|